# 13.2.1 Profil de charge des générateurs
Le profil de charge conventionnel donne pour chaque intervalle de taux de charge le coefficient de pondération correspondant.
### 13.2.1.1 Profil de charge conventionnel
Pour les bâtiments d'habitation, un profil de charge long est considéré (correspond au type d'horaire d'occupation longue).
Le tableau suivant donne le coefficient de pondération pour un profil de charge correspondant à une occupation longue (ex. : logement).
| Taux de charge Tchx | De $0 \%$ <br> à $10 \%$ | De $10 \%$ <br> à $20 \%$ | De $20 \%$ <br> à $30 \%$ | De $30 \%$ <br> à $40 \%$ | De $40 \%$ <br> à $50 \%$ | De $50 \%$ <br> à $60 \%$ | De $60 \%$ <br> à $70 \%$ | De $70 \%$ <br> à $80 \%$ | De $80 \%$ <br> à $90 \%$ | De $90 \%$ <br> à $100 \%$ |
| :----------------------------------------: | :----------------------: | :-----------------------: | :-----------------------: | :-----------------------: | :-----------------------: | :-----------------------: | :-----------------------: | :-----------------------: | :-----------------------: | :------------------------: |
| Coefficient de <br>pondération coeff_pondx | 0,1 | 0,25 | 0,2 | 0,15 | 0,1 | 0,1 | 0,05 | 0,025 | 0,025 | 0 |
Ce profil de charge est donné sur une période de chauffe et non mensuellement. Le calcul du rendement de génération se fera donc sur toute la saison de chauffe et non mensuellement.
Pour les calculs les taux de charge sont pris en milieu de classe $(5 \% ; 15 \% ; 25 \% ; \ldots ; 85 \% ; 95 \%)$,
Le coefficient de pondération $\mathrm{{Coeff}}_{-}\mathrm{{pond}}_{\mathrm{X}}$ est associé au taux de charge $\mathrm{Tch}_{\mathrm{x}}$ qui correspond à l'intervalle $\left[\mathrm{Tch}_{\mathrm{x}}-5 \% ; \mathrm{Tch}_{\mathrm{x}}+5 \%[\right.$
### 13.2.1.2 Présence d'un ou plusieurs générateurs à combustion indépendants
Nous considérerons la présence dans la zone au maximum de N générateurs à combustion indépendants.
Les taux de charge doivent être pondérés par un coefficient **Cdimref** qui permet de prendre en compte les charges partielles.
- Pour un seul générateur à combustion de puissance installée $\mathrm{Pn}_{\text {gen }}$ :
$
\text { Cdimref }=\frac{1000 * \text { Pn gen }}{G V *(\text { Tcons }- \text { Tbase })}
$
- Pour N générateurs à combustion :
$
\text { Cdimref }=\frac{1000 *\left(P n_{g e n_{1}}+P n_{g e n_{2}}+\cdots+P n_{g e n_{N}}\right)}{G V *(\text { Tcons }- \text { Tbase })}
$
Avec :
- $P n_{g e n_{i}}$ puissance installée du générateur à combustion $\mathrm{i}(\mathrm{kW})$
- GV : déperditions totales du bâtiment (W/K)
- Tbase : température extérieure de base $\left({ }^{\circ} \mathrm{C}\right)$
- Tcons : température de consigne $\left(19^{\circ} \mathrm{C}\right.$ en comportement conventionnel et $21^{\circ} \mathrm{C}$ en comportement dépensier)
Les profils de charge conventionnels sont modifiés pour prendre en compte les charges partielles Cdimref, le coefficient $C o e f f_{-}p o n d_{x_{-}d i m}$ est alors affecté au taux de charge $T c h_{\chi_{-}d i m}$, on aura :
$C o e f f_{-}p o n d_{x\_{d i m}}=C o e f f_{-}p o n d_{x}$
Si $\frac{\mathrm{Tch}_{\mathrm{X}}}{\mathrm{Cdimref}}>{1}$, alors sous dimensionnement de l'installation.
Sauf pour le taux de charge $\mathrm{Tch}_{95}$ (correspondant à une charge entre $90 \%$ et $100 \%$ ), on notera :
$
T c h_{95 \_d i m}=T c h_{95}
$
En présence d'un ou de N générateurs indépendants :
- le taux de charge final x de chaque générateur est : $\mathrm{Tch}_{\mathrm{x}_{-} \text {final }}=\mathrm{Tch}_{\mathrm{X}_{-} \text {dim }}$
- ==Le coefficient de pondération final est : Coeff_pond $\mathrm{x}_{\text { final }}$ Coeff_pond $\mathrm{x}_{\text { dim }}$
### 13.2.1.3 Cascade de deux générateurs à combustion
Ne seront traités que les configurations de cascade à deux générateurs. En présence d'une cascade avec plus de deux générateurs, seuls les deux premiers de la cascade seront pris en compte. Aux deux générateurs seront affectés la puissance totale de l'installation. La répartition des puissances des générateurs non retenus sur les 2 générateurs modélisés dans la cascade se fera de façon à maintenir le même ratio de puissance entre les deux.
- Une donnée d'entrée est la puissance relative du générateur i : Prel(gen_i)
- Pn(gen_i) : puissance nominale du générateur i (W)
Dans notre cas avec 2 générateurs :
![[Pasted image 20240909233805.png]]
![[Pasted image 20240909233814.png]]
On détermine pour chaque point de fonctionnement x et pour chaque générateur i sa contribution $\mathrm{CTch}_{\mathrm{x}_{\_} \text {dim }}$(gen_i) au taux de charge du système Tch$\mathrm{x}_{\text { dim }}$ .
### 13.2.1.3.1 Cascade avec priorité
Dans notre cas avec 2 générateurs en cascade, le générateur 1 sera le plus performant ou à défaut le plus puissant, II sera considéré comme prioritaire si aucune information complémentaire n'est disponible :

$
\begin{gathered}
C T c h_{x_{\_} d i m}\left(g e g_{-} 1\right)=\min \left(\operatorname{Prel}\left(\operatorname{gen\_ 1}\right) ; T c h_{x_{\_} d i m}\right) \\
C T c h_{x \_d i m}\left(g e n \_2\right)=\min \left(\text { Prel }\left(g e g_{-} 2\right) ; T c h_{x_{\_} d i m}-C T c h_{x_{\_} d i m}\left(g e n_{-} 1\right)\right)
\end{gathered}
$
Avec le taux de charge final suivant :
![[Pasted image 20240909234048.png]]
![[Pasted image 20240909234057.png]]
![[Pasted image 20240909234105.png]]

### 13.2.1.3.2 Cascade sans priorité (même contribution au taux de charge)
Dans ce cas les générateurs contribuent de manière au taux de charge proportionnellement à leur puissance, on écrira :
![[Pasted image 20240909234138.png]]
![[Pasted image 20240909234146.png]]
Avec le taux de charge final suivant :
![[Pasted image 20240909234234.png]]
![[Pasted image 20240909234245.png]]

![[Pasted image 20240909234259.png]]
Le coefficient de pondération final est :


### 13.2.1.4 Pertes au point de fonctionnement
- $\mathrm{QP}_{\mathrm{x}}(\mathrm{kW})$ : pertes au point de fonctionnement x (taux de charge $\mathrm{x}=\mathrm{Tch}_{\mathrm{x}}$ final )
- $\mathrm{QP}_{0}$ : pertes à l'arrêt (kW)
- $R_{P n}$ et $R_{\text {Pint }}:$ respectivement les rendements à pleine charge et à charge intermédiaire
- Pn : puissance nominale du générateur (kW)
Dans les paragraphes suivants, les rendements à pleine charge Rpn et à charge intermédiaire Rpint sont donnés dans les tableaux en PCI. Cependant, les calculs des rendements de génération sont effectués en PCS (pour éviter d'avoir des rendements
gt;100 \%$ ). Dans les équations pour le calcul du rendement de génération, ils sont donc convertis en PCS (en les divisant par $\mathrm{k}_{P C S / P C I}$ ). Le DPE exprimant les consommations en kWh PCI , les rendements de génération calculés en PCS sont ensuite convertis en PCI pour leur calcul.
De même, les pertes à l'arrêt $Q_{\text {po }}$ et les puissances des veilleuses Pveil sont données pour du PCI. Pour les avoir pour du PCS avant de les utiliser dans les calculs, elles doivent être multipliées par le coefficient de conversion $\mathrm{k}_{P C S / P C I}$
Selon les énergies, le coefficient de conversion en $\mathrm{PCI} / \mathrm{PCS}$ est donné dans le tableau suivant :
| Coefficient de conversion $\mathrm{k}_{P C S / P C I}$ | |
| :---: | :---: |
| Electricité | 1 |
| Gaz naturel | 1,11 |
| GPL | 1,09 |
| Fioul | 1,07 |
| Bois | 1,08 |
| RCU | 1 |
| Charbon | 1,04 |
### 13.2.1.5 Chaudières basse température et condensation :
Pour les chaudières basse température et condensation, le point de fonctionnement w correspond à un fonctionnement à $15 \%$ de charge.
Entre 0 et $15 \%$ de charge :
$
Q P_{x}=\frac{\left[Q P_{15}-0,15 \cdot Q P_{0}\right] * x}{0,15}+0,15 * Q P_{0}
$
Entre 15 et $30 \%$ de charge :
$
Q P_{x}=\frac{\left[Q P_{30}-Q P_{15}\right] * x}{0,15}+Q P_{15}-\frac{\left[Q P_{30}-Q P_{15}\right] * 0,15}{0,15}
$
Entre 30 et $100 \%$ de charge :
$
\begin{gathered}
Q P_{x}=\frac{\left[Q P_{100}-Q P_{30}\right] * x}{0,7}+Q P_{30}-\frac{\left[Q P_{100}-Q P_{30}\right] * 0,3}{0,7} \\
Q P_{15}=\frac{Q P_{30}}{2}
\end{gathered}
$
**Pour les chaudières basse températures:**
- S'il y a une régulation :
![[Pasted image 20240909234513.png]]
- En l'absence de régulation :
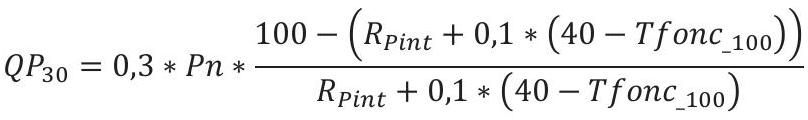
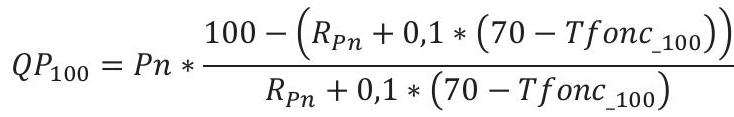
**Pour les chaudières à condensation :**
- S'il y a une régulation :
$Q P_{30}=0,3*P n*\frac{100-\left(R_{P i n t}+0,2*\left(33-T f o n c_{-30}\right)\right)}{R_{P i n t}+0,2*\left(33-T f o n c_{-30}\right)}$
- En l'absence de régulation:
$
Q P_{30}=0,3 * P n * \frac{100-\left(R_{\text {Pint }}+0,2 *\left(33-\text { Tfonc }_{1} 100\right)\right)}{R_{\text {Pint }}+0,2 *\left(33-\text { Tfonc }_{\_} 100\right)}
$
$
Q P_{100}=P n * \frac{100-\left(R_{P n}+0,1 *\left(70-\text { Tfonc }_{1} 100\right)\right)}{R_{P n}+0,1 *(70-\text { Tfonc } 100)}
$
Tfonc_100 $\left({ }^{\circ} \mathrm{C}\right.$ ) est la température de fonctionnement de la chaudière à $100 \%$ de charge. Elle est donnée dans le tableau suivant en fonction des types d'émetteur et des différentes périodes de leur installation :
| | Période | | |
| :---: | :---: | :---: | :---: |
| Température de distribution / Type <br> d'émetteur | Avant 1981 | Entre 1981 et <br> 2000 | Après 2000 |
| Basse / Plancher ou plafond basse <br> température | 60 | 35 | 35 |
| Moyenne / Radiateur à chaleur douce | 80 | 70 | 60 |
| Haute / Autres émetteurs | 80 | 70 | 70 |
Tfonc_ $30\left({ }^{\circ} \mathrm{C}\right.$ ) est la température de fonctionnement de la chaudière à $30 \%$ de charge. Elle est donnée dans les tableaux suivants selon le type d'installation.
**Pour les chaudières à condensation :**
| | Période (émetteurs) | | |
| :------------------------------------------------: | :-----------------: | :---------------------: | :--------: |
| Température de distribution / Type <br> d'émetteur | Avant 1981 | Entre 1981 et <br> 2000 | Après 2000 |
| Basse / Plancher ou plafond basse <br> température | 32 | 24,5 | 24,5 |
| Moyenne / Radiateur à chaleur douce | 38 | 35 | 32 |
| Haute / Autres émetteurs | 38 | 35 | 35 |
**Pour les chaudières basse température :
| | Période (émetteurs) | | |
| :------------------------------------------------: | :-----------------: | :---------------------: | :--------: |
| Température de distribution / Type <br> d'émetteur | Avant 1981 | Entre 1981 et <br> 2000 | Après 2000 |
| Basse / Plancher ou plafond basse <br> température | 42,5 | 35 | 35 |
| Moyenne / Radiateur à chaleur douce | 48,5 | 45,5 | 42,5 |
| Haute / Autres émetteurs | 48,5 | 45,5 | 45,5 |
Si un système de génération alimente des réseaux de distribution de températures différentes, la température de fonctionnement est prise égale à la température maximale.
Pour les installations récentes ou recommandées, les caractéristiques réelles des chaudières présentées sur les bases de données professionnelles peuvent être utilisées.
Si l'année d'installation des émetteurs est inconnue, prendre l'année de construction du bâtiment.
### 13.2.1.6 Chaudières standard
Pour les chaudières standards, le point de fonctionnement w correspond à un fonctionnement à $30 \%$ de charge,
Entre 0 et $30 \%$ de charge :
$
Q P_{x}=\frac{\left[Q P_{30}-0,15 * Q P_{0}\right] * x}{0,3}+0,15 * Q P_{0}
$
Entre 30 et $100 \%$ de charge :
$
Q P_{x}=\frac{\left[Q P_{100}-Q P_{30}\right] * x}{0,7}+Q P_{30}-\frac{\left[Q P_{100}-Q P_{30}\right] * 0,3}{0,7}
$
- S'il y a une régulation
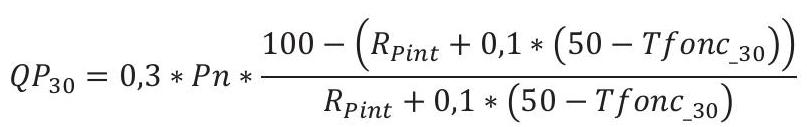
- En l'absence de régulation
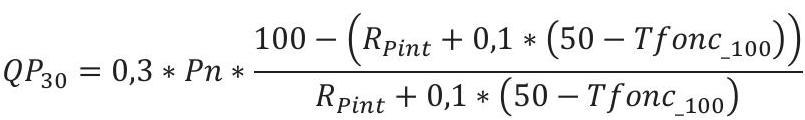
$
\begin{aligned}
& Q P_{100}=P n * \frac{100-\left(R_{P n}+0,1 *\left(70-\text { Tfonc }_{\_} 100\right)\right)}{R_{P n}+0,1 *\left(70-\text { Tfonc }_{\_} 100\right)}
\end{aligned}
$
Avec :
- Tfonc $\_100\left({ }^{\circ} \mathrm{C}\right.$ ) : température de fonctionnement de la chaudière à $100 \%$ de charge. Elle est donnée dans le paragraphe précédent pour les chaudières basse température et condensation
- Tfonc $_{30}\left({ }^{\circ} \mathrm{C}\right)$ : température de fonctionnement de la chaudière à $30 \%$ de charge. Elle est donnée selon le type d'installation dans les tableaux suivants
**Pour une chaudière standard, jusqu'en 1990 :
| | Période (émetteurs) | | |
| :---: | :---: | :---: | :---: |
| Température de distribution / Type <br> d'émetteur | Avant 1981 | Entre 1981 et <br> 2000 | Après 2000 |
| Basse / Plancher ou plafond basse <br> température | 53 | 50 | 50 |
| Moyenne / Radiateur à chaleur <br> douce | 59 | 56 | 53 |
| Haute / Autres émetteurs | 59 | 56 | 56 |
**Pour une chaudière standard, depuis 1991:
| | Période (émetteurs) | | |
| :------------------------------------------------: | :-----------------: | :---------------------: | :--------: |
| Température de distribution / Type <br> d'émetteur | Avant 1981 | Entre 1981 et <br> 2000 | Après 2000 |
| Basse / Plancher ou plafond basse <br> température | 49,5 | 45 | 45 |
| Moyenne / Radiateur à chaleur douce | 55,5 | 52,5 | 49,5 |
| Haute / Autres émetteurs | 55,5 | 52,5 | 52,5 |
Si un système de génération alimente des réseaux de distribution de températures différentes, la température de fonctionnement est prise égale à la température maximale.
Pour les installations récentes ou recommandées, les caractéristiques réelles des chaudières présentées sur les bases de données professionnelles peuvent être utilisées.
Si l'année d'installation des émetteurs est inconnue, prendre l'année de construction du bâtiment.